Inference

$\newcommand{\VS}{\quad \mathrm{VS} \quad}$ $\newcommand{\and}{\quad \mathrm{and} \quad}$ $\newcommand{\E}{\mathbb E}$ $\newcommand{\P}{\mathbb P}$ $\newcommand{\Var}{\mathbb V}$ $\newcommand{\1}{\mathbf 1}$

Estimation of $\beta$

Ordinary Least Square Estimator (OLS)

We observe $Y \in \mathbb R^{n\times 1}$ and $X \in \mathbb R^{n \times p}$.

What is the best estimator $\hat \beta$ of $\beta$ such that $Y = X\beta + \varepsilon$?

Ordinary Least Square (OLS) Estimator:

$\newcommand{\argmin}{\mathrm{argmin}}$

\[\hat \beta = \argmin_{\beta'}\|Y-X\beta'\|^2\]

Here, $\|Y-X\beta'\|^2 = \sum_{i=1}^n(Y_i-\beta_1X_{i}^{(1)}- \dots - \beta_pX_i^{(p)})$

Least squares as an L2 projection

If $\mathrm{rk}(X) = p$, it holds that

\[\hat \beta = (X^TX)^{-1}X^TY\]

$X\hat \beta = X(X^TX)^{-1}X^TY$ is the projection of $Y$ on the space generated by columns of $X$: \[[X]=\mathrm{Im}(X)=\mathrm{Span}(X^{(1)},\dots, X^{(p)})=\{X\alpha, \alpha \in \mathbb R^p\}\]

Least squares as an L2 projection

\[P_{[X]} = X(X^TX)^{-1}X^T \and \widehat{Y} = P_{[X]}Y = X\hat \beta\]

Check that $P_{[X]}$ is the orthogonal projector on $[X]$

That is $P_{[X]}^2 = P_{[X]}$, $P_{[X]}=P_{[X]}^T$ and $\mathrm{Im} (P_{[X]}) = [X]$

Or, without computation:

$P_{[X]}Y$ minimizes $\|Y-Y'\|^2$ over all $Y' \in [X]$.

So $P_{[X]}Y$ must be the orthogonal projection by Pythagorean theorem

Least squares as an L2 projection

We can decompose

\[Y = \underbrace{P_{[X]}Y}_{\widehat Y} + \underbrace{(I-P_{[X]})Y}_{"residuals"}\]

Notice that $I-P_{[X]}= P_{[X]^{\perp}}$ is the orthogonal projection on $[X]^{\perp} = \{\alpha\in \mathbb R^p:~ X\alpha =0\}$

Least squares as an L2 projection

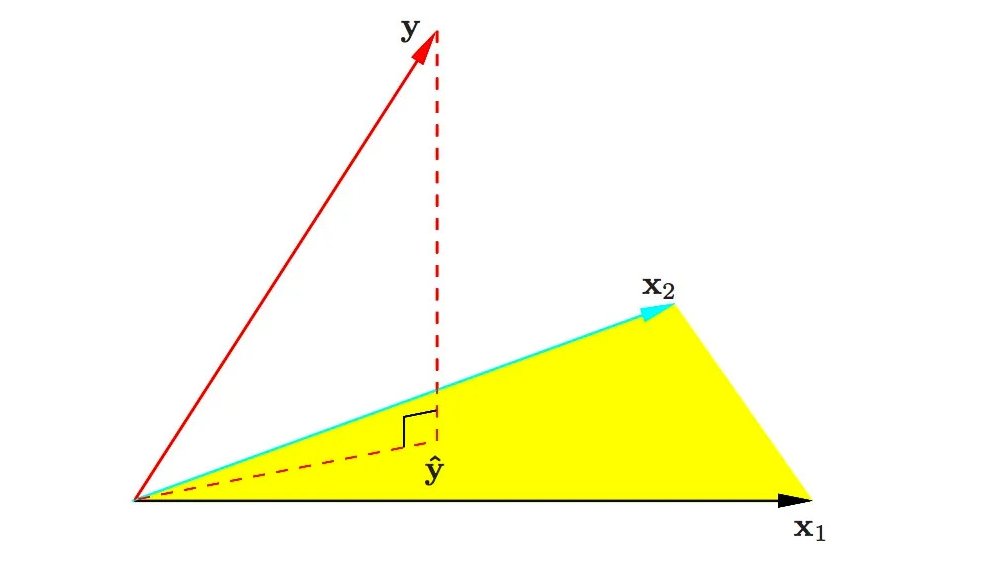
(image: elements of statistical learning. In yellow: $[X]$ with $p=2$)

Properties on $\hat \beta$

Expectation and variance

Assume that $rk(X)=p$, $\mathbb E[\varepsilon] = 0$ and $\mathbb V(\varepsilon) = \sigma^2I_n$. Then,

$\hat \beta = (X^TX)^{-1}X Y$ is a linear estimator
$\mathbb E[\hat \beta] = \beta$ unbiased estimator
$\mathbb V(\hat \beta) = \sigma^2(X^TX)^{-1}$

Gauss-Markov Theorem

Under the same assumptions, if $\tilde \beta$ is another linear and unbiased estimator then \[\mathbb V(\hat \beta) \preceq \mathbb V(\tilde \beta),\]

where $A\preceq B$ means that $B-A$ is a symmetric positive semidefinite matrix Elements of proof

Estimation of $\sigma^2$

Residuals

We define the residuals $\hat \varepsilon$ as

\[ \hat \varepsilon = Y- \hat Y = Y-X\hat \beta \]

It can be computed from the data.

It is the orthogonal projection of $Y$ on $[X]^{\perp}$:

\[Y = \underbrace{P_{[X]}Y}_{\widehat Y} + \underbrace{(I-P_{[X]})Y}_{\hat \varepsilon="residuals"}\]

Residuals

\[ \begin{aligned} Y &= X\beta + \varepsilon & \quad \text{(model)} \\ Y &= \widehat Y + \hat \varepsilon & \quad \text{(estimation)} \end{aligned} \]

Properties on residuals

Expectation and Variance of $\hat\varepsilon$

If $rk(X)=p$, $\mathbb E[\varepsilon] = 0$ and $\mathbb V(\varepsilon)=\sigma^2I_n$, then

$\mathbb E[\hat\varepsilon]=0$
$\mathbb V(\hat \varepsilon) = \sigma^2P_{[X]^\perp} = \sigma^2(I_n - X(X^TX)^{-1}X^T)$

Remark: if a constant vector is in $[X]$, e.g. $\forall i,X_i^{(1)}=1$, then $\hat \varepsilon \perp \mathbf 1$ and

\[ \overline{\hat\varepsilon} = \frac{1}{n}\sum_{i=1}^n \varepsilon_i = 0 \and \overline{\widehat Y} = \overline Y \]

Estimation of $\sigma^2$

Recall that in the model $Y=X\beta + \varepsilon$, both $\beta$ and $\sigma^2=\mathbb E[\varepsilon_i^2]$ are unknown ($p+1$ parameters)

\[ \hat\varepsilon = Y- \hat Y = P_{[X]^\perp}\varepsilon \and dim([X]^{\perp}) = =n-p \]

We estimate $\sigma^2$ with

\[\hat \sigma^2 = \frac{1}{n-p}\sum_{i=1}^n \hat \varepsilon_i^2\]

Properties of $\hat \sigma^2$

Proposition

If $rk(X)=p$, $\E[\varepsilon]=0$ and $\Var(\varepsilon)= \sigma^2I_n$, then

\[\hat \sigma^2 = \frac{1}{n-p}\sum_{i=1}^n \hat \varepsilon_i^2=\frac{\mathrm{SSR}}{n-p}\]

is an unbiased estimator of $\sigma^2$. If moreover the $\varepsilon_i$’s are iid, then $\hat \sigma^2$ is a consistent estimator.

unbiased: $\E[\hat \sigma^2]= \sigma^2$
consistent: $\hat \sigma^2 \to \sigma^2$ a.s. as $n\to +\infty$
SSR: Sum of squared residuals

Gaussian Case

Gaussian Model

Until then, we assumed that $Y=X\beta+\varepsilon$, where $\E[\varepsilon]=0$ and $\Var(\varepsilon)= \sigma^2I_n$.

The $\varepsilon_i$ are uncorrelated but there can be dependency

No assumption was made on the distribution of $\varepsilon$

Now (Gaussian Model):

\[\varepsilon \sim \mathcal N(0, \sigma^2I_n) \quad \text{i.e.} \quad Y \sim \mathcal N(X\beta, \sigma^2I_n)\]

Equivalently we assume that the $\varepsilon_i$’s are iid $\mathcal N(0, \sigma^2)$.

In this simpler model, we can do maximum likelihood estimation (MLE)!

Maximum Likelihood Estimation

MLE

Let $\hat \beta_{MLE}$ and $\hat \sigma_{MLE}^2$ be the MLE of $\beta$ and $\sigma^2$, respectively.

$\hat{\beta}_{MLE} = \hat{\beta}$ et $\hat{\sigma}^2_{MLE} = \frac{SCR}{n} = \frac{n-p}{n} \hat{\sigma}^2$.
$\hat{\beta} \sim N(\beta, \sigma^2(X^TX)^{-1})$.
$\frac{n-p}{\sigma^2} \hat{\sigma}^2 = \frac{n}{\sigma^2} \hat{\sigma}^2_{MLE} \sim \chi^2(n - p)$.
$\hat{\beta}$ and $\hat{\sigma}^2$ are independent

Elements of proof

Efficient Estimator

Theorem

In the Gaussian Model, $\hat \beta$ is an efficient estimator of $\hat \beta$. This means that \[ \Var(\hat \beta) \preceq \Var(\tilde \beta)\; , \] for any estimator $\tilde \beta$. See Elements of proof

This is stronger than Gauss-Markov
Better than any $\tilde \beta$, not only linear $\tilde \beta$. $\hat \beta$ is “BUE” (Best Unbiased Estimator)
If $n$ is large, most of the result in Gaussian case remains valid.

Tests and Confidence Intervals

Pivotal Distribution in Gaussian Case

Recall that $\hat \sigma^2 = \frac{1}{n-p}\|\hat \varepsilon\|^2$

Property

In the Gaussian model,

\[ \frac{\hat \beta_j - \beta_j}{\hat \sigma \sqrt{(X^T X)^{-1}_{jj}}} \sim \mathcal T(n-p) \]

(Student Distribution of degree $n-p$, $(X^TX)^{-1}_{jj}$ is the $j^{th}$ element of the matrix $(X^TX)^{-1}$)

$\mathbb V(\hat{\beta}) = \sigma^2 (X^T X)^{-1}$ implies that $\mathbb V(\hat{\beta}_j) = \sigma^2 (X^T X)^{-1}_{jj}$. $\hat{\sigma}^2_{\hat{\beta}_j}:=\hat\sigma^2 (X^T X)^{-1}$ is an estimator of $\sqrt{\mathbb V(\hat{\beta}_j)}$

Student Signifactivity Test

We observe $Y = X\beta+\varepsilon$, where $\beta \in \mathbb R^p$ is unknown.

We want to test whether the $j^{th}$ feature $X^{(j)}$ is significant in the LM, that is:

$H_0: \beta_j =0 \VS H_1: \beta_j \neq 0$.

We use the test statistic

\[\psi_j(X,Y)= \frac{\hat \beta_j}{\hat \sigma_{\hat \beta_j}} = \frac{\hat \beta_j}{\hat \sigma \sqrt{(X^T X)^{-1}_{jj}}} \sim \mathcal T(n-p) ~~\text{(under $H_0$)}\]

Student Signifactivity Test

\[\psi_j(X,Y)= \frac{\hat \beta_j}{\hat \sigma_{\hat \beta_j}} = \frac{\hat \beta_j}{\hat \sigma \sqrt{(X^T X)^{-1}_{jj}}} \sim \mathcal T(n-p) ~~\text{(under $H_0$)}\]

We reject if $|\psi(X,Y)| \geq t_{1-\alpha/2}$, where $t_{\alpha}$ is the $\alpha$-quantile of $\mathcal T(n-p)$.

\[p_{value}=2\min(F(\psi_j(X,Y)), 1-F(\psi_j(X,Y)))\]

where $F$ is the cdf of $\mathcal T(n-p)$.

If we get $\beta_j=0$, we can remove $X^{(j)}$ from the model.

Confidence Interval

Confidence interval with proba $1-\alpha$ around $\beta_j$:

\[CI_{1-\alpha} = [\hat \beta_j \pm t\hat \sigma_{\hat \beta_j}]\]

Here, $t$ is the $1-\alpha/2$ quantile of $\mathcal T(n-p)$
Recall that $\hat \sigma_{\hat \beta_j} = \hat \sigma \sqrt{(X^T X)^{-1}_{jj}}$

We check that

\[ \P(\beta \in CI_{1-\alpha}) = 1- \alpha \]

Remarks

This is what is computed on $R$
This is valid in Gaussian case, but is also true when $n$ is large for other distributions

Prediction

Prediction Setting

Consider the LM $Y = X\beta + \varepsilon$.

From previous slides, we estimate $(\beta, \sigma)$ with $(\hat \beta, \hat \sigma)$ from observations $Y$ and matrix $X=(X^{(1)}, \dots, X^{(p)})$.

We observe a new individual $o$, with unknown $Y_o$ and vector $X_o=X_{o,\cdot}=(X^{(1)}_o, \dots, X^{(p)}_o)$, and independent noise $\varepsilon_o$.

with this definition, $X_o$ is a row vector and

\[Y_o = X_{o}\beta + \varepsilon_o = \beta_1X^{(1)}_o + \dots + \beta_p X^{(p)}_o+\varepsilon_o\]

Here, $\mathbb E[\varepsilon_o] = 0$ and $\mathbb V(\varepsilon_o)=\sigma^2$

Prediction

We want predict $Y_o$ (unknown) from $X_o$ (known). Natural predictor:

$\hat Y_o = X_o \hat \beta + \varepsilon_o$

Prediction error $Y_o - \hat Y_o$ decomposes in two terms:

\[Y_o - \hat Y_o = \underbrace{X_o(\beta - \hat \beta)}_{\text{Estimation error}} + \underbrace{\varepsilon_o}_{\text{Random error}}\]

Error Decomposition

\[Y_o - \hat Y_o = \underbrace{X_o(\beta - \hat \beta)}_{\text{Estimation error}} + \underbrace{\varepsilon_o}_{\text{Random error}}\]

$\E(Y_o - \hat Y_o)$: prediction error is $0$ on average

\[\begin{aligned} \Var(Y_o - \hat Y_o) &= \color{blue}{ \Var(X_o(\beta - \hat \beta))} + \color{red}{\Var(\varepsilon_o)} \\ &=\color{blue}{\sigma^2X_o(X^TX)^{-1}X_o} + \color{red}{\sigma^2} \\ \end{aligned}\]

$\color{blue}{\Var(X_o(\beta - \hat \beta))\to 0}$ when $n \to +\infty$ but $\color{red}{\Var(\varepsilon_o) =\sigma^2}$

Estimation error is negligible when $n \to +\infty$ but random error is incompressible.

Prediction Interval

In the Gaussian model, $Y_o - \hat Y_o \sim \mathcal N(0, \sigma^2X_o(X^TX)^{-1}X_o^T+\sigma^2)$.

Since $\hat \sigma$ is indep of $\hat Y_o$ (check this with projections!),

\[\frac{Y_o - \hat Y_o}{\hat \sigma\sqrt{X_o(X^TX)^{-1}X_o^T+1}} \sim \mathcal T(n-p)\]

Prediction Interval

We deduce the prediction interval

\[PI_{1-\alpha}(Y_o)=\left[\hat Y_o \pm \sqrt{\color{blue}{\hat \sigma^2X_o(X^TX)^{-1}X_o^T} + \color{red}{\hat \sigma^2}}\right]\]

such that $\P(Y_o \in PI_{1-\alpha})= 1-\alpha$

If we only want to estimate $\mathbb E[Y_o]=X_o \beta$, (point on the hyperplane), we get the confidence interval

\[CI_{1-\alpha}(X_o\beta)=\left[\hat Y_o \pm \sqrt{\color{blue}{\hat \sigma^2X_o(X^TX)^{-1}X_o^T}}\right]\]

Example

For 100 trees, we record their volume and their girth.

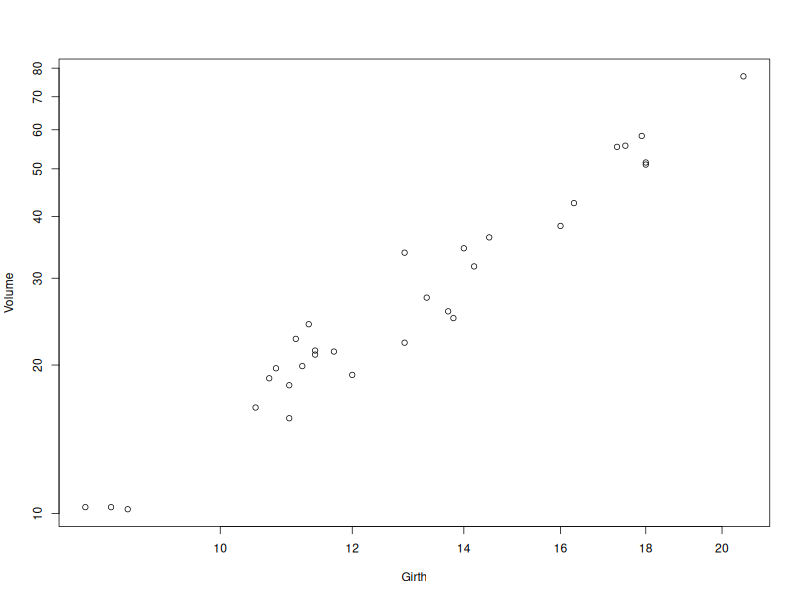
Model

Volume = $\beta_1$ + $\beta_2$ Girth + $\varepsilon$

# In R
reg=lm(Volume ~ Girth, data=trees)
summary(reg)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -36.9435     3.3651  -10.98 7.62e-12 ***
Girth         5.0659     0.2474   20.48  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.252 on 29 degrees of freedom

Results

Estimation:

\[\hat \beta_1=-36.9 \and \hat \beta_2=5.07\] \[\hat \sigma_{\hat \beta_1} =3.4 \and \hat \sigma_{\hat \beta_2} =0.25\]

Statistics:

\[\frac{\hat \beta_1}{\hat \sigma_{\hat \beta_1}}=-10.98 \and \frac{\hat \beta_2}{\hat \sigma_{\hat \beta_2}}=20.48\]

$Pr(>|t|)$: pvalues of the student tests. Last row: $\hat \sigma=4.25$ and df.

Illustration

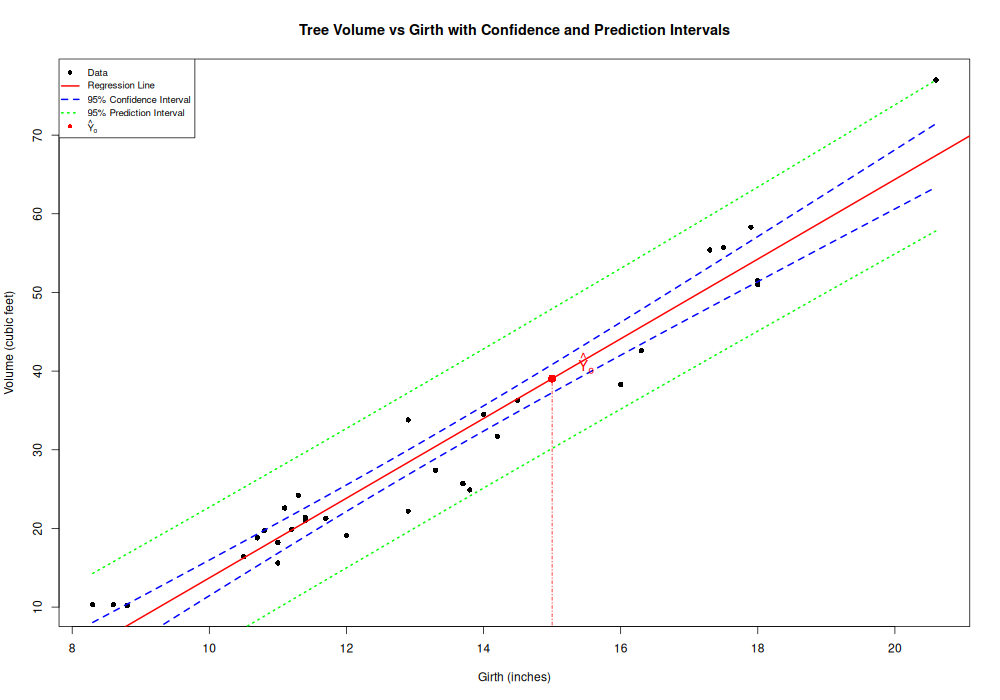
R code

require(stats); require(graphics)
pairs(trees, main = "trees data")
trees[,c("Girth", "Volume")]
reg <- lm(Volume ~ Girth, data = trees)
# Create sequence of x values for smooth curves
x_seq <- seq(min(trees$Girth), max(trees$Girth), length.out = 100)

# Calculate confidence and prediction intervals
conf_int <- predict(reg, newdata = data.frame(Girth = x_seq), 
                   interval = "confidence", level = 0.95)
pred_int <- predict(reg, newdata = data.frame(Girth = x_seq), 
                   interval = "prediction", level = 0.95)

Inference

Estimation of \(\beta\)

Ordinary Least Square Estimator (OLS)

Least squares as an L2 projection

Least squares as an L2 projection

Least squares as an L2 projection

Least squares as an L2 projection

Properties on \(\hat \beta\)

Estimation of \(\sigma^2\)

Residuals

Residuals

Properties on residuals

Estimation of \(\sigma^2\)

Properties of \(\hat \sigma^2\)

Gaussian Case

Gaussian Model

Maximum Likelihood Estimation

Efficient Estimator

Tests and Confidence Intervals

Pivotal Distribution in Gaussian Case

Student Signifactivity Test

Student Signifactivity Test

Confidence Interval

Remarks

Prediction

Prediction Setting

Prediction

Error Decomposition

Prediction Interval

Prediction Interval

Example

Model

Results

Illustration

R code