Analysis of Variance - ANOVA, and of Covariance - ANCOVA

\(\newcommand{\VS}{\quad \mathrm{VS} \quad}\) \(\newcommand{\and}{\quad \mathrm{and} \quad}\) \(\newcommand{\E}{\mathbb E}\) \(\newcommand{\P}{\mathbb P}\) \(\newcommand{\Var}{\mathbb V}\) \(\newcommand{\Cov}{\mathrm{Cov}}\) \(\newcommand{\1}{\mathbf 1}\)

Objective

Link with Previous Lectures

Previously, we considered that:

Response variable \(Y\) is quantitative
Explanatory variables \(X^{(j)}\) are quantitative

We still assume \(Y\) is quantitative, but explanatory variables can be qualitative and/or quantitative.

Terminology

ANOVA (Analysis of Variance): All explanatory variables \(X^{(j)}\) are qualitative
ANCOVA (Analysis of Covariance): Explanatory variables mix both quantitative and qualitative variables

We’ll see that these situations reduce to the case of the previous chapter.

Analysis of Variance with \(1\) Factor

Context, Notations

We seek to explain \(Y\) using a single qualitative variable \(A\).

We observe \((Y, X)\), and define

\[N_i = \sum_{k=1}^n \mathbf 1\{X_k=i\} \and \overline Y_i = \frac{1}{N_i}\sum_{k=1}^n Y_k \mathbf 1\{X_k=i\}\]

Total mean:

\(Y_i = \frac{1}{N}\sum_{k=1}^n Y_k = \frac{1}{N}\sum_{i=1}^I\sum N_i \overline Y_i\)

Setting

For \(k = 1, \ldots, n\)

\[Y_k = \sum_{i=1}^I \mu_i \mathbf{1}\{X_k=A_i\} + \varepsilon_k\]

where \(\E[\varepsilon_k]=0\), \(\Cov(\varepsilon_k,\varepsilon_l)=\sigma^2\1\{k=l\}\)

\(Y_k\) is random and has expectation \(\mu_i\) if \(X_k=A_i\)
\(\Var(Y_k)=\sigma^2\) is the same regardless of modality \(A_i\)

Problem

Do we have \(\mu_1 = \mu_2 \ldots = \mu_I\)? (Does factor \(A\) influences \(Y\)?)
Does a \(\mu_i\) has more influence on \(Y\)?
How do we estimate the \(\mu_i\)’s?

One Hot Encoding

We use one-hot encoding: \(X_{ki}=\1\{X_k=A_i\}\)

That is, for individual \(k\), \(X_{k\cdot} = (\1\{X_k=A_1\}, \dots, \1\{X_k=A_I\}) \in \{0,1\}^I\)

Or, using previous notations, \(X = (X^{(1)}, \dots, X^{(I)})\) where

\[X^{(i)}= \begin{pmatrix} X^{(i)}_1 \\ \vdots \\ X^{(i)}_n \end{pmatrix}\]

In Other Words

If there are \(3\) categories e.g. blue, orange, green, we replace the column \(X\) by \(3\) columns
Example with \(I=3\) categories and \(n=5\) individuals \[ \begin{pmatrix} \color{blue}{\mathrm{blue}} \\ \mathrm{green} \\ \color{blue}{\mathrm{blue}} \\ \mathrm{orange} \\ \mathrm{orange} \\ \end{pmatrix} \quad \text{becomes} \quad X=\begin{pmatrix} \color{blue}{\mathrm{1}} & \mathrm{0} & \mathrm{0}\\ \mathrm{0} & \mathrm{0} & \mathrm{1}\\ \color{blue}{\mathrm{1}} & \mathrm{0} & \mathrm{0}\\ \mathrm{0} & \mathrm{1} & \mathrm{0}\\ \mathrm{0} & \mathrm{1} & \mathrm{0}\\ \end{pmatrix} \]

Model, Matrix Form

We rewrite the model \(Y_k = \sum_{i=1}^I \mu_i \mathbf{1}\{X_k=A_i\} + \varepsilon_k\) as

\[Y = X\mu + \varepsilon\]

Here, \(X_{k\cdot} = (\1\{X_k=A_1\}, \dots, \1\{X_k=A_I\}) \in \{0,1\}^I\)
There is no constant in this model

Model with Constant

If we want to model the constant (intercept) and \(I-1\) modalities, we assume

\[Y_k = \mu_1+\sum_{i=2}^I (\mu_i-\mu_1) \mathbf{1}\{X_k=A_i\} + \varepsilon_k\]

Why \(\mu_i - \mu_1\) and not just \(\mu_i\)?

\(\E[Y_k | X_k=A_i] = \mu_1 + \mu_i - \mu_1 = \mu_i\)
\(\sum_{i=2}^{I}\{X_k = A_i\} = 1\) (collinearity problem)

In R

with intercept (default)

lm(Y~A) #with intercept

Interpretation: gives expectation \(\E[Y_k] = \mu_1\) and coefficients \(\alpha_i= \mu_i - \mu_1\)

without intercept

lm(Y~A-1) #without intercept

Interpretation: gives coefficients \(\alpha_i= \mu_i\)

Estimation of \(\mu\)

Whichever the model we choose (with constant or not), estimation of \(\mu_i=\E[Y_k|X_k=A_i]\) is the same. Same for \(\Var(\varepsilon_k)=\sigma^2\).

Proposition

In category \(i\), OLS estimation of \(\mu_i\) leads to:

\(\hat{\mu}_i = \frac{1}{N_i}\sum_{k=1}^n Y_k \1\{X_k=A_i\} = \overline{Y}_i\)

An unbiased estimator of \(\sigma^2\) is

\(\hat{\sigma}^2 = \frac{1}{n-I} \sum_{k=1}^{n}\sum_{i=1}^I (Y_{k} - \overline{Y}_i)^2\1\{X_k=A_i\}\)

Proof (OLS): derive \(\sum_{k=1}^n (Y_k - \mu'_i)^2\) with respect to \(\mu'_i\)

Testing for Factor Effect (ANOVA Test)

We want to test \(H_0: \mu_1 = \cdots = \mu_I\).

This is a linear constraints test! (See previous chapters)

Proposition

If \(\varepsilon \sim N(0, \sigma^2 I_n)\), then under \(H_0: \mu_1 = \cdots = \mu_I\):

\[F = \frac{SSB/(I-1)}{SSW/(n-I)} \sim F(I-1, n-I)\]

\(SSB = \sum_{i=1}^I N_i (\overline{Y}_i - \overline{Y})^2\)
\(SSW = \sum_{i=1}^I \sum_{k=1}^{n} (Y_{k} - \overline{Y}_i)^2\1\{X_k=A_i\}\)

Critical region at level \(\alpha\): \(RC_\alpha = \{F > f_{I-1,n-I}(1-\alpha)\}\)

Link with previous chapter

In \(\mu_1= \ldots = \mu_I\), there are \(I-1\) constraints to test.

\[F = \frac{n-I}{I-1} \cdot \frac{SSR_c - SSR}{SSR}\]

We show that

\(SSR = SSW\)
\(SSR_c = SST = \sum_{k=1}^n(Y_k - \overline Y)^2\)
\(SST = SSB + SSW\).

In R: anova(lm(Y~A))

Factor Significance: Analysis of Variance Test

Warning

The previous analysis of variance test tests equality of means between modalities not equality of variances

It is valid under the assumption \(\varepsilon \sim N(0, \sigma^2 I_n)\).

Gaussian assumption: Not critical if \(n\) is large
Homoscedasticity: Important assumption

Homoscedasticity Tests

How to test equality of variances in each modality:

Levene test
Bartlett test

In R: leveneTest or bartlett.test from car library

Post-hoc Analysis: Multiple Testing Problem

If factor \(A\) is significant, we want to know more:
which modality(ies) differs from others?

We want to perform all tests:

\[H_{0}^{i,j}: \mu_i = \mu_j \quad \text{vs} \quad H_{1}^{i,j}: \mu_i \neq \mu_j\]

for all \(i \neq j\) in \(\{1, \ldots, I\}\), corresponding to \(I(I-1)/2\) tests.

Multiple Testing: Naive Approach

Perform all Student’s t-tests for mean comparison (1 constraint), each at level \(\alpha\).

Problem: Given the number of tests, this would lead to many false positives.

False positives are a well-known problem in multiple testing.

Solution: Apply a correction to the decision rule, e.g.

Bonferroni correction
Benjamini-Hochberg correction

For one-way ANOVA: Tukey’s test addresses the problem.

Multiple Testing: Tukey’s Test

\[Q = \max_{(i,j)} \frac{|\overline{Y}_i - \overline{Y}_j|}{\hat{\sigma}\sqrt{\frac{1}{N_i} + \frac{1}{N_j}}}\]

Distribution of Tukey’s Test Statistic

Under \(H_0: \mu_1 = \cdots = \mu_I\) and assuming \(\varepsilon \sim N(0, \sigma^2 I_n)\):

\[Q \sim Q_{I,n-I}\]

where \(Q_{I,n-I}\) denotes the Tukey distribution with \((I, n-I)\) degrees of freedom.

Note: This is exact if all \(n_i\) are equal, otherwise the distribution is approximately Tukey.

Individual Tests

To test each \(H_0^{i,j}: \mu_i = \mu_j\), we use the critical regions:

\[RC_\alpha^{i,j} = \left\{|\overline{Y}_i - \overline{Y}_j| > \frac{\hat{\sigma}}{\sqrt{2}} \sqrt{\frac{1}{n_i} + \frac{1}{n_j}} \cdot Q_{I,n-I}(1-\alpha)\right\}\]

where \(Q_{I,n-I}(1-\alpha)\) denotes the \((1-\alpha)\) quantile of a tukey distribution \(Q(I,n-I)\) of degrees \((I, n-I)\).

Key Properties of Tukey’s Test

The form of the previous \(RC_\alpha^{i,j}\) ensures that: \[\mathbb{P}_{\mu_1 = \cdots = \mu_I}\left(\bigcup_{(i,j)} H_1^{i,j}\right) = \alpha\]

Interpretation: If all null hypotheses \(H_0^{i,j}\) are true (\(\mu_1 = \cdots = \mu_I\)), then the probability of concluding at least one \(H_1^{i,j}\) equals \(\alpha\).

This is the simultaneous Type I error rate equals \(\alpha\).

Comparison with Student’s tests

Individual Student’s t-tests at level \(\alpha\): only guarantee \(\mathbb{P}_{\mu_i = \mu_j}(H_1^{i,j}) = \alpha\)
When cumulated: \(\mathbb{P}_{\mu_1 = \cdots = \mu_I}\left[\cup_{(i,j)} H_1^{i,j}\right] \approx 1\) → false positives

Advantage

With Tukey’s test, two significantly different means are truly different, not just due to false positives.

In R: TukeyHSD

Example of R output

Homoscedasticity Test:

leveneTest(Loss∼Exercise)

We get

Levene’s Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 3 0.6527 0.584
68

Homoscedasticity is ok. ANOVA?

reg=lm(Loss∼Exercise) # Exercise has 4 categories
anova(reg)

We get

Response: Loss
         Df Sum Sq Mean Sq F value    Pr(>F)    
Exercise   3 712.56  237.519  20.657 1.269e-09 ***
Residuals 68 781.89   11.498

Results Interpretation

The means are significantly different. We read in particular:

\(I - 1 = 3\), \(n - I = 68\)
\(SSB = 712.56\), \(SSW = 781.89\)
\(F = \frac{SSB/(I-1)}{SSW/(n-I)} = 20.657\)

R Example: Post-hoc Analysis

We finish by analyzing the mean differences more precisely:

TukeyHSD(aov(Loss~Exercise))

Exercise
     diff        lwr        upr     p adj
2-1  7.1666667   4.1897551 10.1435782 0.0000001
3-1  3.8888889   0.9119773  6.8658005 0.0053823
4-1 -0.6111111  -3.5880227  2.3658005 0.9487355
3-2 -3.2777778  -6.2546894 -0.3008662 0.0252761
4-2 -7.7777778 -10.7546894 -4.8008662 0.0000000
4-3 -4.5000000  -7.4769116 -1.5230884 0.0009537

Conclusion: All differences are significant, except between exercise 4 and exercise 1.

Analysis of Variance with \(2\) Factors

Setting

We observe \(Y\) and explanatory variables \(X^{(1)}, X^{(2)}\)

\(X^{(1)}_k \in \{A_1, \dots, A_I\}\) (\(I\) modalities)
\(X^{(2)}_k \in \{B_1, \dots, B_J\}\) (\(J\) modalities)
\(N_{ij} = \sum_{k=1}^n \1\{X^{(1)}_k \in A_i\}\1\{X_k^{(2)} \in B_j\}\) individuals in modality \(A_i\) and \(B_j\)

Model

\[\begin{aligned} Y_k &= m + \alpha_i\sum_{i=1}^I\1\{X^{(1)}_k \in A_i\} +\beta_i\sum_{j=1}^J\1\{X^{(2)}_k \in B_j\} \\ &+ \gamma_{ij}\sum_{i=1}^I\sum_{j=1}^J\1\{X^{(1)}_k \in A_i\}\1\{X^{(2)}_k \in B_i\} + \varepsilon_k \end{aligned}\]

In other words, in modality \(A_i\) and \(B_j\),

\(Y_k =m+\alpha_i + \beta_j + \gamma_{ij}+ \varepsilon_k\)

Interpretation

This is a model of the type \(Y_k = \mu_{ij} + \varepsilon_k\).

In modalities \((i,j)\), \(\E[Y_k] = \mu_{ij} = m + \alpha_i + \beta_j + \gamma_{ij}\)

\(m\): the average effect of \(Y\) (without considering \(A\) and \(B\))
\(\alpha_i = \mu_{i.} - m\): the marginal effect due to \(A\)
\(\beta_j = \mu_{.j} - m\): the marginal effect due to \(B\)
\(\gamma_{ij} = \mu_{ij} - m - \alpha_i - \beta_j\): the remaining effect, due to interaction between \(A\) and \(B\)

Example 1

\(Y\): employee satisfaction
\(A\): schedule type (flexible or fixed)
\(B\): training level (basic or advanced)

We can imagine:

Effect due to \(A\): satisfaction is greater with flexible schedules
Effect due to \(B\): satisfaction is higher with advanced training
No particular interaction between A and B

Example 2

\(Y\): plant yield
\(A\): fertilizer type (1 or 2)
\(B\): water quantity (low, medium, high)

We can imagine:

Effect due to \(A\): yield differs according to fertilizer used
Effect due to \(B\): yield is better when there is lots of water
Interaction: fertilizer 1 is better with water, and vice versa for fertilizer 2

Maybe interaction is so strong that the effect due to A seems absent!

Constraints on the Parameters

In modalities \((i,j)\), \(\E[Y_k] = \mu_{ij} = m + \alpha_i + \beta_j + \gamma_{ij}\)

Initial two-factor ANOVA problem: \(I \times J\) parameters \(\mu_{ij}\).

Now: \(1 + I + J + IJ\) parameters (\(m\), \(\alpha_i\), \(\beta_j\), \(\gamma_{ij}\)).

Therefore, we need \(1 + I + J\) constraints for identifiability:

\(\sum_{i=1}^{I} \alpha_i = 0 \and \sum_{j=1}^{J} \beta_j = 0\)

\(\sum_{i=1}^{I} \gamma_{ij} = 0 \and \sum_{j=1}^{J} \gamma_{ij} = 0\)

These constraints ensure model identifiability by removing the redundant parameters that cause multicollinearity issues.

Implementation in R

The complete model (with interaction) is launched with the command:

lm(Y ~ A + B + A:B) ## or equivalently, lm(Y ~ A*B)

With these constraints, the parameter interpretation is as follows:

Intercept: \(m = \mu_{11}\)
Main effect A: \(\alpha_i = \mu_{i1} - \mu_{11}\)
Main effect B: \(\beta_j = \mu_{1j} - \mu_{11}\)
Interaction: \(\gamma_{ij} = \mu_{ij} - \mu_{i1} - \mu_{1j} + \mu_{11}\)

Important Note on Interpretation

From

lm(Y ~ A + B + A:B) ## or equivalently, lm(Y ~ A*B)

Be Cautious on the Interpretation of the Coefficients

To impose the constraints from the previous approach (sum-to-zero constraints):

lm(Y ~ A*B, contrasts = list(A = contr.sum, B = contr.sum))

Estimation

The choice of constraints does not affect the estimation of the expectation of \(Y\) in each crossed modality \(A_i \cap B_j\).

Proposition

Whatever the linear constraints chosen, the OLS leads to, for all \(i = 1, \ldots, I\), \(j = 1, \ldots, J\) and \(k = 1, \ldots, N_{ij}\), if \(X^{(1)}_{k}=A_i\) and \(X_k^{(2)}=B_j\):

\[\widehat{Y}_{k} = \overline{Y}_{ij}:= \frac{1}{N_{ij}} \sum_{k=1}^{n} Y_{k}\1\{X_k^{(1)}=A_i \and X_k^{(2)}=B_j\}\]

and to the estimation of the residual variance:

\[\hat{\sigma}^2 = \frac{1}{n - IJ} \sum_{i=1}^I\sum_{j=1}^J\sum_{k=1}^n (Y_{k} - \overline{Y}_{ij})^2\1\{X_k^{(1)}=A_i \and X_k^{(2)}=B_j\}\]

Significance Tests for Effects

Is the effect due to the interaction between A and B significant?
Is the marginal effect due to A significant?
Is the marginal effect due to B significant?

First, in the additive model with interaction, \(Y_{ijk} = m + \alpha_i + \beta_j + \varepsilon_{ijk}\)

Do we have \(\gamma_{ij} = 0\) for all \(i, j\)?

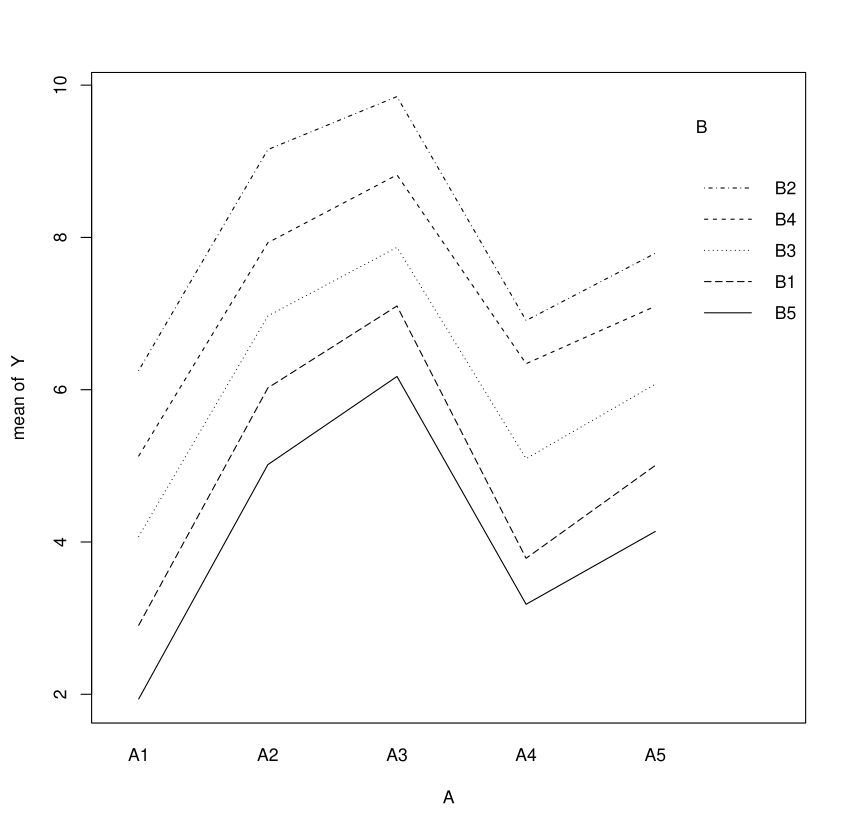
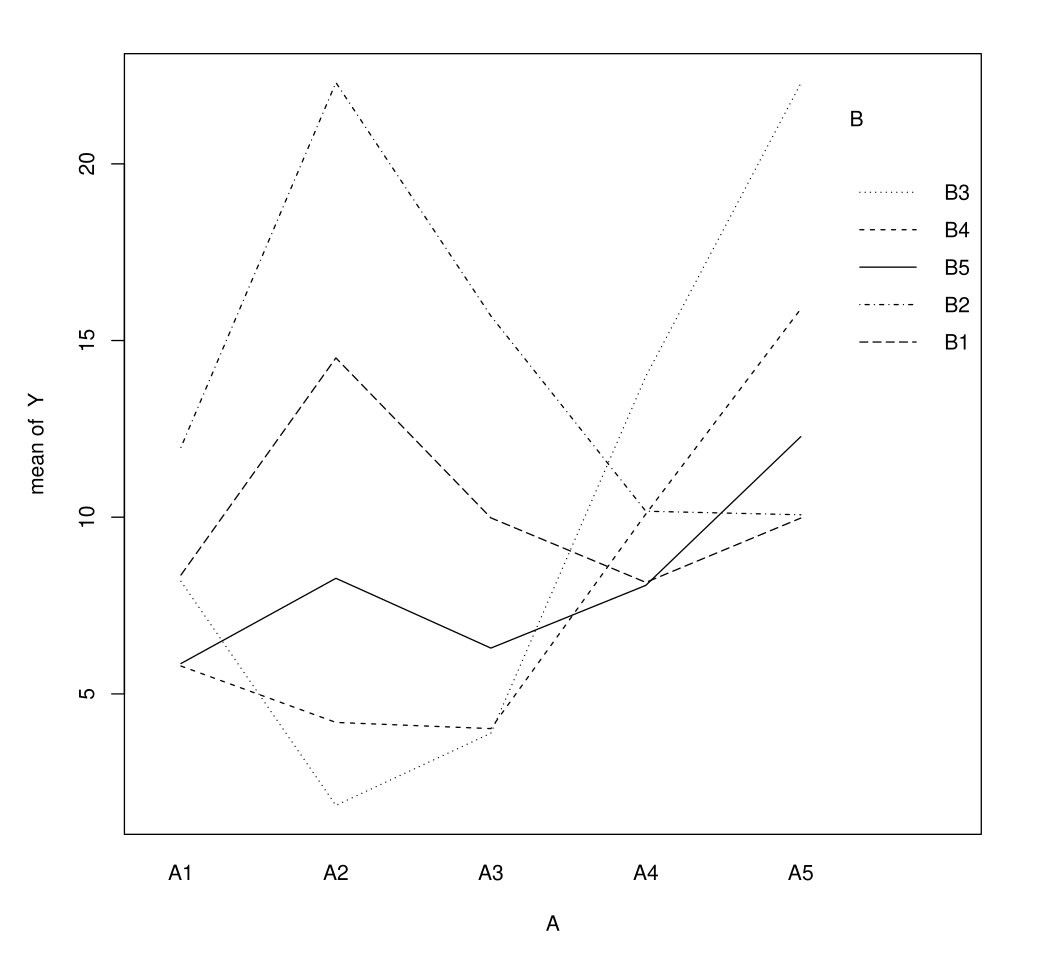
Interpretation on Plots:

Plot \(\overline Y_{ij}\) in function of modalities \((i,j)\)

without interactions, lines should be almost parallel

interaction.plot(A,B,Y)

Plot: Presence of Interaction

Lines cross in presence of interaction

Significance Tests

We want to test for the presence of an interaction:

\[H_0^{(AB)}: \gamma_{ij} = 0 \text{ for all } i, j\]

If we conclude \(H_0^{(AB)}\) (accept the null hypothesis), we then want to test the marginal effects:

\[H_0^{(A)}: \alpha_i = 0 \text{ for all } i \and H_0^{(B)}: \beta_j = 0 \text{ for all } j\]

Presence of Interaction

\[H_0^{(AB)}: \gamma_{ij} = 0 \text{ for all } i, j\]

Warning

If we reject \(H_0^{(AB)}\), it makes no sense to test whether A or B have an effect: they have one through their interaction.

These tests reduce to constraint tests in the regression model.

Balanced Design Analysis of Variance

We assume that “the design is balanced”: this means that \(N_{ij}:=N\) does not depend on \(i\) or \(j\). (Otherwise, everything becomes complicated).

In this case, we have the analysis of variance formula:

ANOVA Formula

\[S_T^2 = S_A^2 + S_B^2 + S_{AB}^2 + S_R^2\]

\(S_T^2 = \sum_{k=1}^{n} (Y_{k} - \overline{Y})^2\): total sum of squares
\(S_A^2 = \sum_{i=1}^{I} \sum_{j=1}^{J} N_{ij} (\overline{Y}_{i.} - \overline{Y})^2\): \(S^2_{between}\) in the case of one-factor ANOVA where the factor is \(A\)
\(S_B^2 = \sum_{i=1}^{I} \sum_{j=1}^{J} N_{ij} (\overline{Y}_{.j} - \overline{Y})^2\): \(S^2_{between}\) in the case of one-factor ANOVA where the factor is \(B\)
\(S_{AB}^2 = \sum_{i=1}^{I} \sum_{j=1}^{J} N_{ij} (\overline{Y}_{ij} - \overline{Y}_{i.} - \overline{Y}_{.j} + \overline{Y})^2\) quantifies the interaction
\(S_R^2 = \sum_{i=1}^{I} \sum_{j=1}^{J} \sum_{k=1}^{N_{ij}} (Y_{k} - \overline{Y}_{ij})^2\1\{X^{(1)}_k=A_i \and X^{(2)}_k=B_j\}\): \(S_{within}\) in one-factor ANOVA

Testing the Interaction

For testing the interaction, \(H_0^{(AB)}: \gamma_{ij} = 0\) for all \(i, j\)

We the linear constraint test statistic \(F = \frac{n-p}{q} \frac{(SSR_c - SSR)}{SSR}\)

where \(SSR_c\) corresponds to the sum of squares of the residuals in the space \(\gamma_{ij}=0\) for all \((i,j)\).

\[F^{(AB)} = \frac{S_{AB}^2/(I-1)(J-1)}{S_R^2/(n-IJ)}\]

When \(\varepsilon \sim \mathcal N(0, \sigma^2 I_n)\), \(F^{(AB)} \sim \mathcal F((I-1)(J-1), n-IJ)\)

Testing the Effect of \(A\)

For testing the main effect of \(A\), \(H_0^{(A)}: \alpha_i = 0\) for all \(i\):

We use \(F = \frac{n-p}{q} \frac{(SSR_c - SSR)}{SSR}\)

where \(SSR_c\) corresponds to the sum of squares of the residuals in the space \(\alpha_i=0\) for all \(i\).

\[F^{(A)} = \frac{S_A^2/(I-1)}{S_R^2/(n-IJ)}\]

When \(\varepsilon \sim \mathcal{N}(0, \sigma^2 I_n)\), \(F^{(A)} \sim \mathcal{F}(I-1, n-IJ)\)

Testing the Effect of \(B\)

For testing the main effect of \(B\), \(H_0^{(B)}: \beta_j = 0\) for all \(j\):

We use \(F = \frac{n-p}{q} \frac{(SSR_c - SSR)}{SSR}\)

where \(SSR_c\) corresponds to the sum of squares of the residuals in the space \(\beta_j=0\) for all \(j\).

\[F^{(B)} = \frac{S_B^2/(J-1)}{S_R^2/(n-IJ)}\]

When \(\varepsilon \sim \mathcal{N}(0, \sigma^2 I_n)\), \(F^{(B)} \sim \mathcal{F}(J-1, n-IJ)\)

R outputs

In software, these tests are summarized in a table as shown below.

In R: anova(lm(Y ~ A*B))

Source	df	Sum Sq	Mean Sq	F value	Pr(>F)
\(A\)	\(I-1\)	\(S_A^2\)	\(S_A^2/(I-1)\)	\(F^{(A)}\)	…
\(B\)	\(J-1\)	\(S_B^2\)	\(S_B^2/(J-1)\)	\(F^{(B)}\)	…
\(A:B\)	\((I-1)(J-1)\)	\(S_{AB}^2\)	\(S_{AB}^2/((I-1)(J-1))\)	\(F^{(AB)}\)	…
Residuals	\(n-IJ\)	\(S_R^2\)	\(S_R^2/(n-IJ)\)

Two-Factor ANOVA Practice

Assumptions

Fisher tests are based on the assumption \(\varepsilon \sim N(0, \sigma^2 I_n)\)

Normality is not critical, but homoscedasticity is
We can test equality of variances in each modality of A (or B), or in each crossed modality if the \(n_{ij}\) are sufficiently large
This can be done with Levene’s test or Bartlett’s test

Practical Procedure

Test equality of variances
Form the ANOVA table (independent of chosen constraints)
If the \(AB\) interaction is significant: don’t change anything
If the interaction is not significant: analyze the marginal effects of A and B

If they are significant: the model is additive: lm(Y ~ A + B)
Otherwise: we can remove \(A\) (or \(B\)) from the model

Post-Hoc Analysis

Once effects are identified: perform post-hoc analysis by examining differences between (crossed) modalities more closely, using Tukey’s test as in one-factor ANOVA

Multi-Factor Analysis with Qualitative Variables

Principle and Limits

We seek to explain \(Y\) using \(k\) qualitative variables \(A=X^{(1)}\), \(B=X^{(2)}\), \(C=X^{(3)}\), …

We can assume that \(\E[Y_k]\) depends on each factor and their interactions:

Two-way interactions: \(AB\), \(BC\), \(AC\), etc.
Three-way interactions: \(ABC\), etc.
Higher-order interactions: and potentially more

Warning

This results in \(2^k - 1\) possible effects for \(k\) factors.

Testing Approach

Each effect can be tested using linear constraint tests. However, this approach presents several challenges:

Multiple testing burden: Too many tests to perform
Sample size limitations: Risk of insufficient sample sizes in each crossed modality

In practice, choices are made to include only a limited number of effects and interactions in the analysis.

Covariance Analysis - ANCOVA

Model Components

Most general situation: we seek to explain Y using both quantitative and qualitative variables.

Quantitative variable effects: Through each regression coefficient \(\beta_j\) associated with each variable

Factor effects and interactions: As in ANOVA analysis

Main effects of factors (quali. var.)
Interactions between factors

Mixed interactions: Effects of interactions between factors and quantitative variables

Example of Mixed Interaction

\(A \in \{\text{Labrador}, \text{Chihuaha}\}\)
\(X^{(1)}\): size of the dog
There is clearly a mixed interraction between factor \(A\) and \(X^{(1)}\)!

Statistical Testing

Each effect can be tested using a Fisher test.
Obviously, choices must be made regarding which effects and interactions to include in the model.

Linear Models in R: Quantitative and Qualitative Variables

Model Without Interaction

\(Y\): quantitative response variable

\(X\): quantitative variable,

\(Z\): factor with \(I\) modalities \(\{A_1, \dots, A_I\}\)

lm(Y~X+Z) estimates the model without interaction, where, for each individual \(k = 1, \ldots, n\):

\[Y_k = m + \beta X_k + \sum_{i=2}^{I} \alpha_i \mathbf{1}\{Z_k=A_i\} + \varepsilon_k\]

Constraint \(\alpha_1 = 0\) is adopted to make the model identifiable.

Model With Interaction

lm(Y~X+A+X:A) or lm(Y~X*A) estimates the model with interaction:

\[ \begin{aligned} Y_k &= m + \beta X_k + \sum_{i=2}^{I} \beta_i X_k \mathbf{1}\{Z_k=A_i\} \\ &+ \sum_{i=2}^{I} \alpha_i \mathbf{1}\{Z_k=A_i\} + \varepsilon_k \end{aligned} \]

Key Insight: In the interaction model, the coefficient \(\beta\) associated with \(X\) varies according to the modality \(A_i\).