Correlation, Homogeneity and Dependency
Correlation Test
- We observe iid paired data \((X_1, Y_1), \dots, (X_n,Y_n)\) of unknown mean \(\mu_X, \mu_Y\) and cov matrix \(\Sigma\). Let \(X=X_1\), \(Y=Y_1\).
- \(\mathrm{Cov(X,Y)} = \mathbb E[(X- \mathbb E[X])(Y- \mathbb E[Y])]\)
- \(H_0: \mathrm{Cov}(X,Y)=0\) or \(H_1: \mathrm{Cov}(X,Y)\neq 0\)
- \(\sigma_X^2 = \mathrm{Cov(X,X)}\)
- \(\sigma_Y^2 = \mathrm{Cov(Y,Y)}\)
- \(\mathrm{Cor(X,Y)} = \frac{\mathrm{Cov(X,Y)}}{\sigma_X \sigma_Y}\) [Wooclap]
- Cov matrix: \(\Sigma = \left(\begin{matrix} \sigma_X^2 & \mathrm{Cov(X,Y)} \\ \mathrm{Cov(X,Y)} & \sigma_Y^2 \\ \end{matrix}\right)\)
Pearson’s Correlation Test
\(r = \frac{\sum_{i=1}^n (X_i - \overline X)(Y_i - \overline Y)}{\sqrt{\sum_{i=1}^n (X_i - \overline X)^2\sum_{i=1}^n (Y_i - \overline Y)^2}}\)
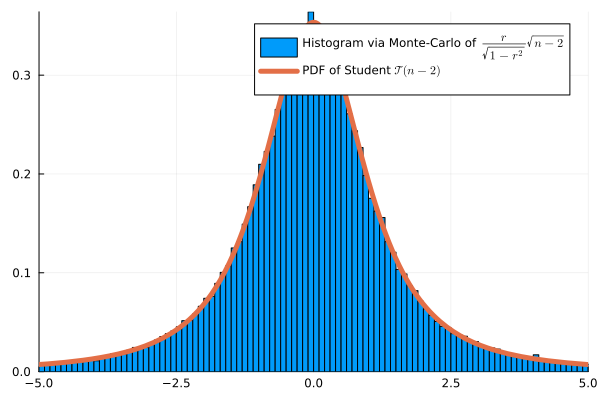
\(\psi(X,Y) = \frac{r}{\sqrt{1-r^2}}\sqrt{n-2}\)
Under \(H_0\), \(\psi(X,Y) \approx \mathcal T(n-2)\)
Correlation Test
Monte Carlo Simulation with \(n=4\):
ANOVA Test
- \(d\) independent groups (bags), each containing \(N_1, \dots, N_d\) individuals. \(N_{\mathrm{tot}} = \sum_{k=1}^d N_k\)
- Group \(k\): \((X_{1,k}, \dots, X_{N_k,k}) \in \mathbb R^{N_k}\) are iid \(\mathcal N(\mu_k, \sigma)\). Ex: \(X_{ik} =\) sallary of \(i\) living in region \(k\) [Wooclap]
- \(H_0: \mu_1 = \dots = \mu_d\) vs \(H_1: \mu_l \neq \mu_k\) for some \((l,k)\) (unknown \(\sigma\))
ANOVA
- Empirical mean of group \(k\): \(\overline X_k = \tfrac{1}{N_k}\sum_{i=1}^{N_k} X_{ik}\) [Wooclap]
- Sum of Squares in group \(k\):
\(SS_k = \sum_{i=1}^{N_k} (X_{ik} - \overline X_k)^2 \sim \sigma^2\chi^2(N_k-1)\) (under \(H_0\)) - Empirical var of group \(k\): \(V_k = \tfrac{1}{N_k}SS_k\)
- Total empirical mean: \(\overline X = \tfrac{1}{N_{\mathrm{tot}}}\sum_{k=1}^d\sum_{i=1}^{N_k} X_{ik}\)
- Sum of Squares btween Groups: \(SSB = \sum_{k=1}^{d} N_k(\overline X_k - \overline X)^2\sim\sigma^2\chi^2(d-1)\) (under \(H_0\))
ANOVA Test Statistic
- \(\psi(X) = \frac{\tfrac{1}{N_{\mathrm{tot}} - d}\sum_{k=1}^d SS_k}{\tfrac{1}{d-1}SSB}\)
- \(\psi(X) \sim \mathcal F(N_{\mathrm{tot}}-d, d-1)\) (Fisher under \(H_0\))
- Two-sided test: double the min left/right \(p_{value}\).
Interpretation of variances in ANOVA
\[ \left.\begin{array}{cl} \overline X_k &= \frac{1}{N_k} \sum_{i=1}^{N_k} X_{ik}\\ \overline{X} &= \frac{1}{N_{\mathrm{tot}}} \sum_{k=1}^d N_k\overline X_{k},&\end{array}\right. \left.\begin{array}{cl} V_k &= \frac{1}{N_k}\sum_{i=1}^{N_k} (X_{ik} - \overline X_k)^2 \\ V_W &= \frac{1}{N_{\mathrm{tot}}} \sum_{k=1}^d N_kV_k\\ V_B &= \frac{1}{N_{\mathrm{tot}}}\sum_{i=1}^{N_k} N_k(\overline X_k - \overline X)^2\\ V_{T} &= \frac{1}{N_{\mathrm{tot}}}\sum_{k=1}^d\sum_{i=1}^{N_k} (X_{ik} - \overline X)^2 \end{array} \right. \]
- \(V_k\): Empirical variance of group \(k\)
- \(V_W\): Average empirical variance within groups (unexplained variance)
- \(V_B\): Empirical variance between groups (explained variance)
- \(V_T\): Total variance of the sample
\[\psi(X) = \frac{\tfrac{1}{N_{\mathrm{tot}} - d}\sum_{k=1}^d SS_k}{\tfrac{1}{d-1}SSB}=\frac{\tfrac{1}{N_{tot}-d}V_W}{\tfrac{1}{d-1}V_B} = \frac{d-1}{N_{tot}-d} \frac{V_W}{V_B} \sim \mathcal F(N_{tot}-d, d-1) \; .\]
\(\chi^2\) Homogeneity and Independence Tests
\(\chi^2\) Homogeneity Test
- \(d\) different bags (or groups), each containing balls of \(m\) potential colors.
- If \(d = 3\) and \(m=2\), we observe the following \(2\times 3\) matrix of counts:
| bag 1 | bag 2 | bag 3 | Total | |
|---|---|---|---|---|
| color 1 | \(X_{11}\) | \(X_{12}\) | \(X_{13}\) | \(R_1\) |
| color 2 | \(X_{21}\) | \(X_{22}\) | \(X_{23}\) | \(R_2\) |
| Total | \(N_1\) | \(N_2\) | \(N_3\) | \(N\) |
- Bag \(j\): \((X_{1j}, X_{2j}) \sim \mathrm{Mult}(N_j, (p_{1j}, p_{2j}))\)
- The parameters \(p_{ij}\) are unknown [Wooclap]
- \(H_0\): \(p_{i1} = p_{i2}=p_{i3}\) for all color \(i\) (bags are homogeneous)
- \(H_1\): bags are heterogeneous
- \(\sum_{i=1}^m\sum_{j=1}^d \frac{(X_{ij}- N_jp_{ij})^2}{N_jp_{ij}}\) not a test statistic
Chi-Squared Homogeneity Test Statistic
- \(\hat p_{i} = \tfrac{1}{N}\sum_{j=1}^{d}X_{ij} = \frac{R_i}{N}\)
- \(\psi(X) = \sum_{i=1}^m\sum_{j=1}^d \frac{(X_{ij}- N_j\hat p_{i})^2}{N_j\hat p_{i}}\)
- Approximation: \(\psi(X) \sim \chi^2((m-1)(d-1))\)
Example: Soft drink preferences
- Split population into \(3\) categories: Young Adults (18-30), Middle-Aged Adults (31-50), and Seniors (51 and above).
- \(H_0\): The groups are homogeneous in terms of soft drink preferences
| Age Group | Young Adults | Middle-Aged | Seniors | Total |
|---|---|---|---|---|
| Coke | 60 | 40 | 30 | 130 |
| Pepsi | 50 | 55 | 25 | 130 |
| Sprite | 30 | 45 | 55 | 130 |
| Total | 140 | 140 | 110 | 390 |
- \(N_1 \hat p_1 = 140*\frac{130}{390} \approx 46.7\)
\[ \begin{aligned} \psi(X) &= \frac{(60-46.7)^2}{46.7}&+ \frac{(40-46.7)^2}{46.7}&+\frac{(30-36.7)^2}{36.7} \\ &+\frac{(50-46.7)^2}{46.7}&+ \frac{(55-46.7)^2}{46.7}&+\frac{(25-36.7)^2}{36.7}\\ &+\frac{(30-46.7)^2}{46.7}&+ \frac{(45-46.7)^2}{46.7}&+\frac{(55-36.7)^2}{36.7}\\ &\approx 26.57 \end{aligned} \]
\(\chi^2\) Independence Test
- Observations: Paired Categorical Variables \((X_1, Y_1), \dots, (X_n, Y_n)\)
- e.g. \(X_i \in \{\mathrm{male}, \mathrm{female}\}\), \(Y_i \in \{\mathrm{coffee}, \mathrm{tea}\}\) [Wooclap]
- Idea: regroup the data into bags, e.g. \(\{\mathrm{male}, \mathrm{female}\}\)
- Build the contingency table
- Perform a chi-square homogeneity test
Example of contingency table:
| Gender | Male | Female | Total |
|---|---|---|---|
| Coffee | 30 | 20 | 50 |
| Tea | 28 | 22 | 50 |
| Total | 58 | 42 | 100 |
Expected counts:
| Gender | Male | Female | Total |
|---|---|---|---|
| Coffee | 29 | 21 | 50 |
| Tea | 29 | 21 | 50 |
| Total | 58 | 42 | 100 |
- \(N_1 \hat p_1 = 58 \cdot 50/100 = 29\)
- Degree of freedom: \((2-1)(2-1) = 1\)
Wilcoxon’s Signed Rank
Symetric Random Variable
- A median of \(X\) is a \(0.5\)-quantile of its distribution
- If \(X\) has density \(p\), the median \(m\) is such that \[ \int_{-\infty}^m p(x)dx = \int_{m}^{+\infty} p(x)dx = 0.5 \; . \]
- A symmetric random variable \(X\) is such that the distribution of \(X\) is the same as the distribution of \(-X\).
- In particular, its median is \(0\).
- If \(X\) is a symmetric random variable, then it has the same distribution as \(\varepsilon |X|\) where \(\varepsilon\) is independent of \(X\) and uniformly distributed in \(\{-1,1\}\)
Symetrization
- If \(X\) and \(Y\) are two independent variables with same density \(p\), then \(X-Y\) is symetric.
- Indeed: \[ \begin{aligned} \mathbb P(X - Y \leq t) &=\int_{-\infty}^t \mathbb P(X \leq t+y)p(y)dy =\int_{-\infty}^t \mathbb P(Y \leq t+x)p(x)dy = \mathbb P(Y-X \leq t) \; . \end{aligned} \]
- \(X\) indep of \(Y\) \(\implies\) \(X-Y\) symmetric \(\implies\) \(\mathrm{median}(X-Y) = 0\)
Dependency Problem for Paired Data
We observe iid pairs of real numbers \((X_1, Y_1), \dots, (X_n, Y_n)\). The density of each pair \((X_i, Y_i)\) is unknown \(p_{XY}(x,y)\).
The marginal distribution of \(X_i\) and \(Y_i\) are, respectively, \[p_X(x) = \int_{y \in \mathbb R} p_{XY}(x,y)~~~~ \text{ and }~~~~ p_{Y}(y) = \int_{x \in \mathbb R} p_{XY}(x,y) \; .\]
\(H_0:\) The median of \((X_i - Y_i)\) is \(0\) for all \(i\)
\(H_1:\) The median of \((X_i - Y_i)\) is not \(0\) for some \(i\) [Wooclap]
Generality of \(H_0\)
- If \(X_i-Y_i\) is symmetric \(i\), then we are under \(H_0\).
- If \(X_i\) is independent of \(Y_i\) for all \(i\), then we are under \(H_0\).
Warning
- The pairs are assume to be independent, but within each pair, \(Y_i\) can depend on \(X_i\) (that is, we don’t necessarily have \(p(x,y) =p_X(x)p_Y(y)\)).
Wilcoxon’s Signed Rank Test
- \(D_i = X_i - Y_i\)
- We define the sign of pair \(i\) as the sign of \(D_i=X_i - Y_i\). It is in \(\{-1, 1\}\).
- We define the rank of pair \(i\) as the permutation \(R_i\) that satisfies \(|D_{R_i}| = |D_{(i)}|\), where [Wooclap] \[ |D_{(1)}| \leq \dots \leq |D_{(n)}| \]
Properties on the Signed Ranks
Under \(H_0\),
Signs of the \((D_i)\)’s are independent and uniformly distributed in \(\{-1, 1\}\).
In particular, the number of signs equal to \(+1\) follows a Binomial distribution \(\mathcal B(n,0.5)\).
The ranks \(R_i\) of the \((|D_i|)\)’s does not depend on the unknown density \(p_{X-Y}\). \((R_1, \dots, R_n)\) is a random permutation under \(H_0\).
Hence, any deterministic function of the ranks and of the differences is a pivotal test statistic: it does not depend on the distribution of the data under \(H_0\).
Wilcoxon’s Signed Rank Test
Properties on the Signed Ranks
- Wilcoxon’s test statistic: \(W_- = \sum_{i=1}^n R_i \mathbf 1\{D_i < 0\}\)
- Sometimes, also \(W_+ = \sum_{i=1}^n R_i \mathbf 1\{D_i > 0\}\) or \(\min(W_-, W_+)\).
- Gaussian approximation: \(W_- \asymp n(n+1)/4 + \sqrt{n(n+1)(2n+1)/24} \mathcal N(0,1)\)
- if \(H_1\): \(\mathrm{median}(D_i) > 0\): left-tailed test on \(W_-\).
This approximation fits well the exact distribution. Monte-Carlo simulation:
Effect of Drug on Blood Pressure
- \(H_0\): the drug has no effect. \(H_1\): it lowers the blood pressure
| Patient | \(X_i\) (Before) | \(Y_i\) (After) | \(D_i = X_i-Y_i\) | \(R_i\) |
|---|---|---|---|---|
| 1 | 150 | 140 | 10 | 6 (+) |
| 2 | 135 | 130 | 5 | 5 (+) |
| 3 | 160 | 162 | -2 | 2 (-) |
| 4 | 145 | 146 | -1 | 1 (-) |
| 5 | 154 | 150 | 4 | 4 (+) |
| 6 | 171 | 160 | 11 | 7 (+) |
| 7 | 141 | 138 | 3 | 3 (+) |
- \(W_- = 1+2 = 3\).
- From a simulation, we approx \(\mathbb P(W_-=i)\), for \(i \in \{0, 1, 2, 3, 4, 5,6\}\) under \(H_0\) by
[0.00784066, 0.00781442, 0.00781534, 0.01563892, 0.01562184, 0.02343478]- From a simulation, \(p_{value}=\mathbb P(W_- \leq 3) \approx 0.039 < 0.05\)